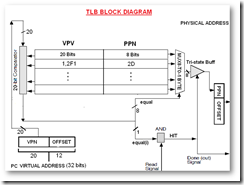
I had an assignment to implement RSA algorithm, according to our textbook, the steps are like below

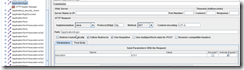
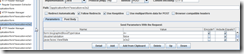
I have made my form so that user can enter the values of the prime numbers, p, q, and the public key, e, or the user can press on a buttons to generate these numbers randomly, I have made it very simple, with no validations, and encrypting only numbers below the length n of the RSA algorithm.
I have called the text fields p,q,e,d,m,c with IDs txtP, txtQ, txtE, txtD, txtM, txtC
To generate random p, and q, I am using a function RandomIntegerBelow (which I created with the help of some posts from stackoverflow) to generate a random BigInteger below a specific number then test if this number is prime or not using Rabin Millar test(I posted it in previous post) , and keep looping until I get it
private void btnGenerateP_Click(object sender, EventArgs e)
{
BigInteger p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
while (!IsProbabilyPrime(p, 20))
{
p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
}
txtP.Text = p.ToString();
}
To get random e, I generated a random number below totient and tested if gcd(totient, e) = 1, and looped until I get it.
private void btnGenerateE_Click(object sender, EventArgs e)
{
log("generating e randomely such that gcd(e,totient) = 1");
BigInteger temp = 0;
while (GCD_Euclidean(temp, BigInteger.Parse(txtTOT.Text)) != 1)
{
temp = RandomIntegerBelow(BigInteger.Parse(txtTOT.Text));
log("new E = " + temp);
}
txtE.Text = temp.ToString();
}
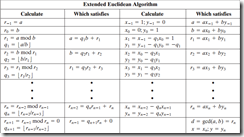
I used the function Extended_GCD (I have posted in in previous post) to get the modulo multiplicative inverse for the e value to get d, this function returns array of the values gcd, x, y respectively that satisfies gcd(m,n) = m*x + n*y, and I am reading always y as my answer since I am sending the totient first then the value of e.
private void btnCalculateD_Click(object sender, EventArgs e)
{
BigInteger[] result = new BigInteger[3];
result = Extended_GCD(BigInteger.Parse(txtTOT.Text), BigInteger.Parse(txtE.Text));
if (result[2] < 0)
result[2] = result[2] + BigInteger.Parse(txtTOT.Text);
txtD.Text = result[2].ToString();
}
Now I have e,d,n (public key, private key, length) which are the important parameters for RSA algorithm
Lastly, to encrypt and decrypt
private void btnEncrypt_Click(object sender, EventArgs e)
{
log("Encrypting, C = M^e mod n");
txtC.Text = BigInteger.ModPow(BigInteger.Parse(txtM.Text), BigInteger.Parse(txtE.Text), BigInteger.Parse(txtN.Text)).ToString();
}
private void btnDecrypt_Click(object sender, EventArgs e)
{
log("Encrypting, M' = C^d mod n");
txtMR.Text = BigInteger.ModPow(BigInteger.Parse(txtC.Text), BigInteger.Parse(txtD.Text), BigInteger.Parse(txtN.Text)).ToString();
}
Below is the full code including the helper functions
private void btnGenerateP_Click(object sender, EventArgs e)
{
BigInteger p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
while (!IsProbabilyPrime(p, 20))
{
p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
}
txtP.Text = p.ToString();
}
private void btnGenerateQ_Click(object sender, EventArgs e)
{
BigInteger p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
while (!IsProbabilyPrime(p, 20))
{
p = RandomIntegerBelow(BigInteger.Parse(txtMax.Text));
}
txtQ.Text = p.ToString();
}
private void btnCalculateD_Click(object sender, EventArgs e)
{
BigInteger[] result = new BigInteger[3];
result = Extended_GCD(BigInteger.Parse(txtTOT.Text), BigInteger.Parse(txtE.Text));
if (result[2] < 0)
result[2] = result[2] + BigInteger.Parse(txtTOT.Text);
txtD.Text = result[2].ToString();
}
private void btnCalculateN_Click(object sender, EventArgs e)
{
log("N = P*Q = " + txtP.Text + " x " + txtQ.Text);
txtN.Text = (BigInteger.Multiply(BigInteger.Parse(txtP.Text), BigInteger.Parse(txtQ.Text))).ToString();
}
private void btnCalculateTOT_Click(object sender, EventArgs e)
{
log("totient = (P-1)*(Q-1) = " + (BigInteger.Parse(txtP.Text) - 1) + " x " + (BigInteger.Parse(txtQ.Text) - 1));
txtTOT.Text = (BigInteger.Multiply(BigInteger.Parse(txtP.Text) - 1, BigInteger.Parse(txtQ.Text) - 1)).ToString();
}
private void btnGenerateE_Click(object sender, EventArgs e)
{
log("generating e randomely such that gcd(e,totient) = 1");
BigInteger temp = 0;
while (GCD_Euclidean(temp, BigInteger.Parse(txtTOT.Text)) != 1)
{
temp = RandomIntegerBelow(BigInteger.Parse(txtTOT.Text));
log("new E = " + temp);
}
txtE.Text = temp.ToString();
}
private void btnEncrypt_Click(object sender, EventArgs e)
{
log("Encrypting, C = M^e mod n");
txtC.Text = BigInteger.ModPow(BigInteger.Parse(txtM.Text), BigInteger.Parse(txtE.Text), BigInteger.Parse(txtN.Text)).ToString();
}
private void btnDecrypt_Click(object sender, EventArgs e)
{
log("Encrypting, M' = C^d mod n");
txtMR.Text = BigInteger.ModPow(BigInteger.Parse(txtC.Text), BigInteger.Parse(txtD.Text), BigInteger.Parse(txtN.Text)).ToString();
}
#region helpers
public void log(string s)
{
txtLog.Text += s + "\r\n";
}
public static BigInteger GCD_Loop(BigInteger A, BigInteger B)
{
BigInteger R = BigInteger.One;
while (B != 0)
{
R = A % B;
A = B;
B = R;
}
return A;
}
public BigInteger GCD_Euclidean(BigInteger A, BigInteger B)
{
log("gcd(" + A + "," + B + ")");
if (B == 0)
return A;
if (A == 0)
return B;
if (A > B)
return GCD_Euclidean(B, A % B);
else
return GCD_Euclidean(B % A, A);
}
public bool IsProbabilyPrime(BigInteger n, int k)
{
bool result = false;
if (n < 2)
return false;
if (n == 2)
return true;
// return false if n is even -> divisbla by 2
if (n % 2 == 0)
return false;
//writing n-1 as 2^s.d
BigInteger d = n - 1;
BigInteger s = 0;
while (d % 2 == 0)
{
d >>= 1;
s = s + 1;
}
for (int i = 0; i < k; i++)
{
BigInteger a;
do
{
a = RandomIntegerBelow(n - 2);
}
while (a < 2 || a >= n - 2);
if (BigInteger.ModPow(a, d, n) == 1) return true;
for (int j = 0; j < s - 1; j++)
{
if (BigInteger.ModPow(a, 2 * j * d, n) == n - 1)
return true;
}
result = false;
}
return result;
}
public BigInteger RandomIntegerBelow(int n)
{
var rng = new RNGCryptoServiceProvider();
byte[] bytes = new byte[n / 8];
rng.GetBytes(bytes);
var msb = bytes[n / 8 - 1];
var mask = 0;
while (mask < msb)
mask = (mask << 1) + 1;
bytes[n - 1] &= Convert.ToByte(mask);
BigInteger p = new BigInteger(bytes);
return p;
}
public BigInteger RandomIntegerBelow(BigInteger bound)
{
var rng = new RNGCryptoServiceProvider();
//Get a byte buffer capable of holding any value below the bound
var buffer = (bound << 16).ToByteArray(); // << 16 adds two bytes, which decrease the chance of a retry later on
//Compute where the last partial fragment starts, in order to retry if we end up in it
var generatedValueBound = BigInteger.One << (buffer.Length * 8 - 1); //-1 accounts for the sign bit
var validityBound = generatedValueBound - generatedValueBound % bound;
while (true)
{
//generate a uniformly random value in [0, 2^(buffer.Length * 8 - 1))
rng.GetBytes(buffer);
buffer[buffer.Length - 1] &= 0x7F; //force sign bit to positive
var r = new BigInteger(buffer);
//return unless in the partial fragment
if (r >= validityBound) continue;
return r % bound;
}
}
public BigInteger[] Extended_GCD(BigInteger A, BigInteger B)
{
BigInteger[] result = new BigInteger[3];
bool reverse = false;
if (A < B) //if A less than B, switch them
{
BigInteger temp = A;
A = B;
B = temp;
reverse = true;
}
log("Extended GCD");
BigInteger r = B;
BigInteger q = 0;
BigInteger x0 = 1;
BigInteger y0 = 0;
BigInteger x1 = 0;
BigInteger y1 = 1;
BigInteger x = 0, y = 0;
log(A + "\t" + " " + "\t" + x0 + "\t" + y0);
log(B + "\t" + " " + "\t" + x1 + "\t" + y1);
while (A % B!=0)
{
r = A % B;
q = A / B;
x = x0 - q * x1;
y = y0 - q * y1;
x0 = x1;
y0 = y1;
x1 = x;
y1 = y;
A = B;
B = r;
log(B + "\t" + r + "\t" + x + "\t" + y);
}
result[0] = r;
if (reverse)
{
result[1] = y;
result[2] = x;
}
else
{
result[1] = x;
result[2] = y;
}
return result;
}
public BigInteger Extended_GCD2(BigInteger n, BigInteger m)
{
BigInteger[] Quot = new BigInteger[50];
bool reverse = false;
if (n < m)
{
BigInteger z;
z = n;
n = m;
m = z;
reverse = true;
}
BigInteger originaln = n;
BigInteger originalm = m;
int xstep = 1;
BigInteger r = 1;
while (r != 0)
{
BigInteger q = n / m;
r = n - m * q;
log(" " + n + " = " + m + "*" + q + " + " + r);
n = m;
m = r;
Quot[xstep] = q;
++xstep;
}
//setgcd(n)
BigInteger gcd = n;
BigInteger a = 1;
BigInteger b = 0;
for (int i = xstep; i > 0; i--)
{
BigInteger z = b - Quot[i] * a;
b = a;
a = z;
}
return a;
}
#endregion